Czy obserwacja cieni może mieć coś wspólnego z matematyką? Czy może stanowić podstawę do obliczeń, rysunków, kształtowania umiejętności matematycznych?
Rozważania na ten temat można zacząć tradycyjnie: „już Tales i Pitagoras … „ lub „ już małe dzieci …” . Zacznijmy od dzieci. Każdy bowiem, nawet małe dzieci, w słoneczny dzień może zaobserwować cienie drzew, budynków, czy też cienie swoje i swoich kolegów. Cień może być tematem zajęć w szkole lub w terenie, a zrozumienie własności cieni prowadzi do wielu dziedzin matematyki i jej zastosowań.
Jeśli źródło światła jest bardzo odległe, tak jak w przypadku Ziemi i Słońca, to promienie słoneczne uznajemy za równoległe. Obserwowane cienie to rzuty równoległe przestrzennych obiektów na powierzchni ziemi. O własnościach rzutowania pisze Zdzisław Pogoda w siedemnastym tomiku serii „Miniatury matematyczne” p.t. „Zabawy z cieniem”. Tomik przeznaczony jest dla uczniów szkół ponadgimnazjalnych, a jego lektura wymaga pewnego zasobu wiedzy matematycznej. Dobrze jest jednak kształcić pewne intuicje i wrażliwość matematyczną od najmłodszych lat.
Japońscy twórcy Megumi Kajiwara i Tathuhiko Nijima stworzyli dla najmłodszych interaktywną historię opowiadaną cieniem. Między stronami książki umieszczone są wycinanki. Oświetlając je pod różnym kątem, otrzymujemy ruchome obrazy, które „opowiadają” indywidualne historie.
Efekty można obejrzeć np. na stronie :http://www.lustrobiblioteki.pl/search?q=motion+silhouette.

tumblr_mbplmffRxo1ribmt4o1_1280.jpg
„Lektura” tej niezwykłej pozycji rozbudza wyobraźnię i zmysł obserwacji najmłodszych i może być inspiracją do własnych zajęć z cieniem. Jest tu też okazja do kształcenia matematycznego: pytania o to czy cienie wiernie oddają kształt przedmiotów, czy zachowują wielkość, prowadzą do intuicyjnego rozumienia ważnych własności rzutowania. Łatwo jest bowiem zauważyć, że cienie nie oddają wiernie kształtu (rzutowanie nie zachowuje miary kątów) i nie zachowują wielkości (rzutowanie nie zachowuje długości odcinków, ale zachowuje ich proporcje).
„Cieniasy”, wbrew pozorom, nie są przeznaczone dla tych, którzy cienko sobie radzą z matematyką. Nazwa tej pomocy nie pochodzi bowiem od przymiotnika „cienki” , ale właśnie od cienia. Jest to zestaw manipulacyjny ilustrujący rzutowanie prostopadłe.

Źródło: http://www.matematyka.wroc.pl/programykomputerowe/cieniasy
Modele walca, graniastosłupa i prostopadłościanu to elementy służące do budowania różnych konstrukcji, których cienie pokazane są na stronach dołączonej do zestawu książeczki. Dysponując taką pomocą, można poprzez zabawę kształtować wyobraźnię przestrzenną uczniów. Można oczywiście budować własne zestawy, np. z modeli brył czy przedmiotów codziennego użytku.
Ćwiczenie: Wybierz potrzebne ci przedmioty i zbuduj konstrukcję, której cienie na prostopadłych kartkach wyglądają jak na rysunkach:

Uczniowie mogą łączyć wybrane przedmioty np. za pomocą plasteliny lub masy mocującej.
Podczas zajęć w terenie, obserwacje cieni, jakie rzucają kije o równych lub różnych długościach, umożliwiają zauważenie ważnych prawidłowości, które pozwolą lepiej zrozumieć własności rzutu równoległego i ułatwią sporządzanie rysunków brył:

Łatwo jest na przykład zauważyć, że:
Równe i równoległe kije rzucają równe i równoległe cienie (rzutem odcinków równych i równoległych są odcinki równe i równoległe).
Cień dłuższego kija jest zawsze dłuższy od cienia kija krótszego, cień kija dłuższego np. dwa razy jest dwa razy dłuższy od cienia kija krótszego (rzut równoległy zachowuje proporcje odcinków).
Analiza rysunków sporządzonych na podstawie obserwacji może stanowić punkt wyjścia do wprowadzenia definicji funkcji trygonometrycznych kąta ostrego:
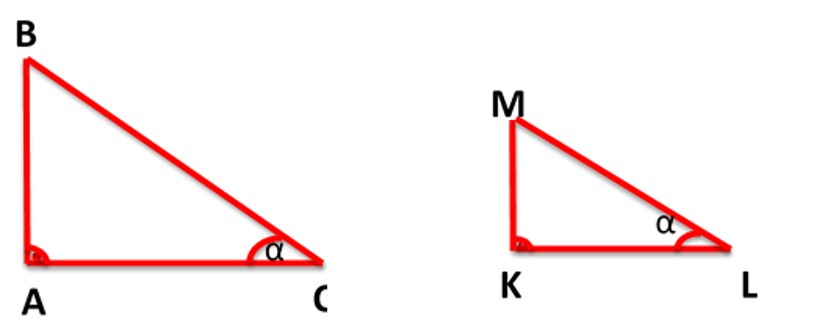
W danej chwili kąt padania promieni słonecznych α jest taki sam, a więc trójkąty ACB i KLM są podobne. Stosunek odpowiednich boków w trójkątach podobnych jest taki sam, a więc:
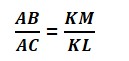
Iloraz ten to tangens kąta α. Wprowadzając następne ilorazy definiujemy pozostałe funkcje trygonometryczne kąta ostrego α.
Idąc śladem cienia, matematyczne rozważania można również rozpocząć od starożytnych Greków. Uważa się, że to Tales był prekursorem naukowego badania rzeczywistości w oparciu o obserwacje natury i rozum. Talesowi właśnie przypisuje się wykorzystanie cienia do naukowych rozważań. Uznawany jest on za pierwszego matematyka, chociaż matematyką zajmował się przede wszystkim w celach praktycznych. Diogenes Laertios twierdził, że Tales potrafił określić wysokości egipskich piramid i obliczyć odległość od brzegu statków na morzu. To właśnie obserwacje cienia pozwoliły mu na wyznaczenie wysokości piramidy.
Tales wiedział, że Słońce podobnie traktuje wszystkie rzeczy, zarówno człowieka, jak i potężną piramidę, zatem zauważał: stosunek pomiędzy mną a moim cieniem jest dokładnie taki sam jak pomiędzy piramidą a jej cieniem. Stąd wniosek: w chwili, w której mój cień będzie równy mojej wysokości, cień piramidy będzie równy jej wysokości!
Do rozwiązania pozostaje jeszcze jeden problem: nie widzimy, a tym samym nie możemy zmierzyć cienia całej wysokości piramidy, jego część chowa się w podstawie piramidy. Z drugiej strony w chwili, gdy długość cienia będzie równa długości przedmiotu, długość „ukrytej” części cienia będzie równa połowie krawędzi podstawy piramidy!
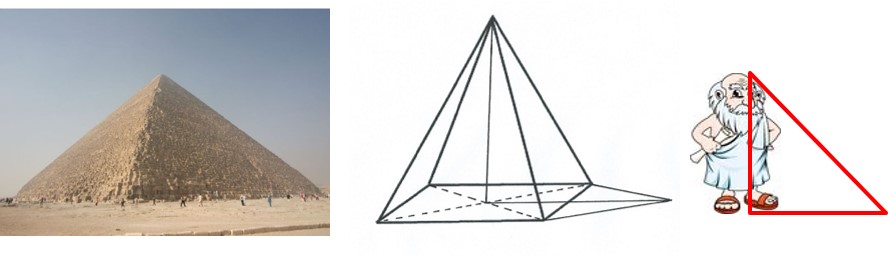
Ćwiczenie: Starożytni Grecy nie używali ujednoliconej jednostki długości i zwykle mierzyli rzeczy większe za pomocą mniejszych. Tales w pomiarach często używał siebie jako „mniejszą rzecz”, czyli jednostkę . Ponoć Tales ustalił wysokość piramidy Cheopsa na 85 „talesów” . Wysokość piramidy po wybudowaniu to 146,59 m (współcześnie w wyniku erozji i utraty wieńczącego szczyt piramidionu liczy 138,75 m). Oblicz wzrost Talesa.
Wyznaczenie wysokości drzewa, jest łatwiejsze bo możemy zmierzyć długości całości cienia. Po co nam wiedza na ten temat? Na przykład dla zaspokojenia ciekawości albo do … rozwiązania zagadki kryminalnej. Nawet detektyw nad detektywami Sherlock Holmes stosował z powodzeniem sposób Talesa. Wykorzystał przy tym wskazówki z tajemniczego dokumentu rodu Musgraveów:

Oczywiście Sherlock Holmes znał i wykorzystał sposób Talesa i mógł pochwalić się Watsonowi w jaki sposób rozwiązał zagadkę.

Powyższy fragment opowiadania A. C. Doyle’a może stanowić wstęp do zadania o wyznaczaniu wysokości drzewa.
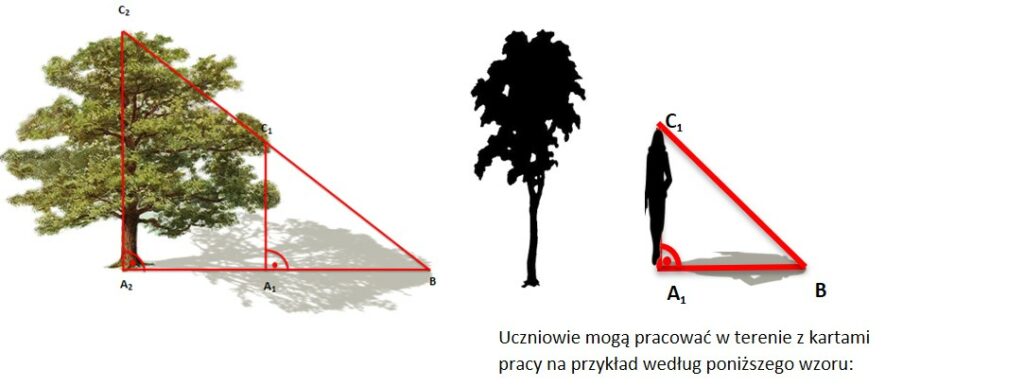
Zadanie: Oblicz wysokość wybranego drzewa.
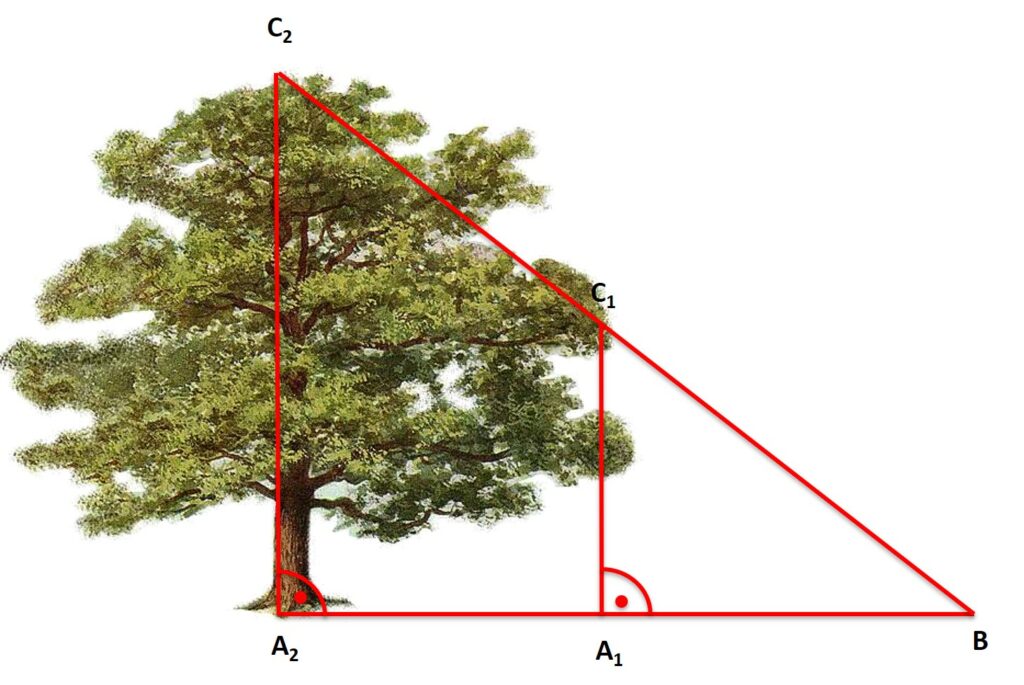
INFORMACJE: W wybranym miejscu, o określonej porze długość przedmiotu i długość jego cienia, to wielkości wprost proporcjonalne. Znaczy to, że drzewo (odcinek A2C2) jest tyle samo razy dłuższe /krótsze od swojego cienia A2B , ile razy inny obiekt (na przykład ty , a na rysunku odcinek A1C1) jest dłuższy/ krótszy od swojego cienia A1B.
INSTRUKCJA (dzieci młodsze):
- Zmierz długość swojego cienia.
Długość mojego cienia wynosi… - Zmierz długość cienia wybranego drzewa.
Długość cienia drzewa wynosi … - Mój wzrost wynosi …
- Oblicz ile razy jesteś większy /mniejszy od długości twojego cienia:
mój wzrost : długość mojego cienia = [ ] - Drzewo jest również tyle samo razy większe/mniejsze od swojego cienia, ile razy ty jesteś większy/mniejszy od swojego cienia. Oblicz więc jego wysokość:
wysokość drzewa = długość cienia ∙ [ ]
- Zmierz długość swojego cienia.
Długość mojego cienia wynosi… - Zmierz długość cienia wybranego drzewa.
Długość cienia drzewa wynosi … - Mój wzrost wynosi …
- Oblicz ile razy jesteś większy /mniejszy od długości twojego cienia:
mój wzrost : długość mojego cienia = [ ] - Drzewo jest również tyle samo razy większe/mniejsze od swojego cienia, ile razy ty jesteś większy/mniejszy od swojego cienia. Oblicz więc jego wysokość:
wysokość drzewa = długość cienia ∙ [ ]
INSTRUKCJA (dzieci starsze): Zmierz długość swojego cienia. Długość mojego cienia wynosi …
Zmierz długość cienia wybranego drzewa.
Długość cienia drzewa wynosi …
Mój wzrost wynosi …
Ułóż odpowiednią proporcję. Proporcja: …
Rozwiąż równanie zapisane w postaci proporcji i odpowiedz na pytanie jak wysokie jest drzewo?
Długość cienia drzewa wynosi …
Druga część zajęć to „Tajemnice cienia” Krystyny Raczkowskiej – Tomczak
Bibliografia:
[1]. Anne Rooney, Fascynująca matematyka, Bellona, Warszawa 2011
[2]. Zdzisław Pogoda, Zabawy z cieniem, Miniatury matematyczne , Aksjomat, Toruń 2005
[3]. Artur Conan Doyle, Księga wszystkich dokonań Sherlocka Holmesa, Re, Warszawa 2011
[4]. http://www.lustrobiblioteki.pl
[5]. http://www.matematyka.wroc.pl/
[6]. http://supermatma.w.interia.pl/menu/tales1.html
Fotografia wyróżniająca: https://pixabay.com/pl/photos/łąka-góry-krajobraz-natura-2774061/
Autor: Aleksandra Opaska
Publikowane: Opaska Aleksandra; Biuletyn Polskiego Stowarzyszenia Nauczycieli Przedmiotów Przyrodniczych, „W cieniu z matematyką”, Nauczanie Przedmiotów Przyrodniczych, 2/2015, Toruń 2015, s. 21-20