„Nauka wokół nas” to jedno podstawowych założeń prowadzonych przez nas w ramach Laboratorium Nauk Przyrodniczych Eureka, a dawniej Centrum Nauk Przyrodniczych. Na naszych zajęciach staramy się zachęcać dzieci do obserwowania i poznawania otoczenia. Najbardziej rozpowszechnioną cieczą na Ziemi jest woda. Wodę pijemy, kąpiemy się w niej, podlewamy nią nasze pola, wykorzystujemy w przeróżnych dziedzinach gospodarki, może być ona groźna w czasie powodzi i ratunkiem w czasie suszy. Jest niezbędnym warunkiem istnienia naszego życia i cywilizacji. Prawie 71% powierzchni kuli ziemskiej pokrywa woda. Wydaje się więc, że jej zasoby są ogromne, ale aż 97% z tego to woda słona. No to w końcu mamy dostatek wody, czy też jej zasoby są skromne? Amerykańska Agencja Geologiczna USGS przygotowała wizualizację, która odpowiada na to pytanie. Gdyby całą wodę występującą na naszej planecie zamknąć w kuli, to kula ta miałaby średnicę 1384 km, dla porównania średnica kuli ziemskiej to średnio 12 742 km. Niestety, ze względu na zasolenie, ziemskie zasoby wody zdatnej do picia zmieszczą się w kuli o średnicy 273 km, z czego tylko niewielka część jest dostępna dla ludzi. Jeżeli pominiemy zapasy wody gruntowej to nasze zasoby wody pitnej zmieszczą się w kuli o średnicy zaledwie 56 km! Na grafice przygotowanej przez USGS obrazuje to prawie niewidoczna kropeczka.
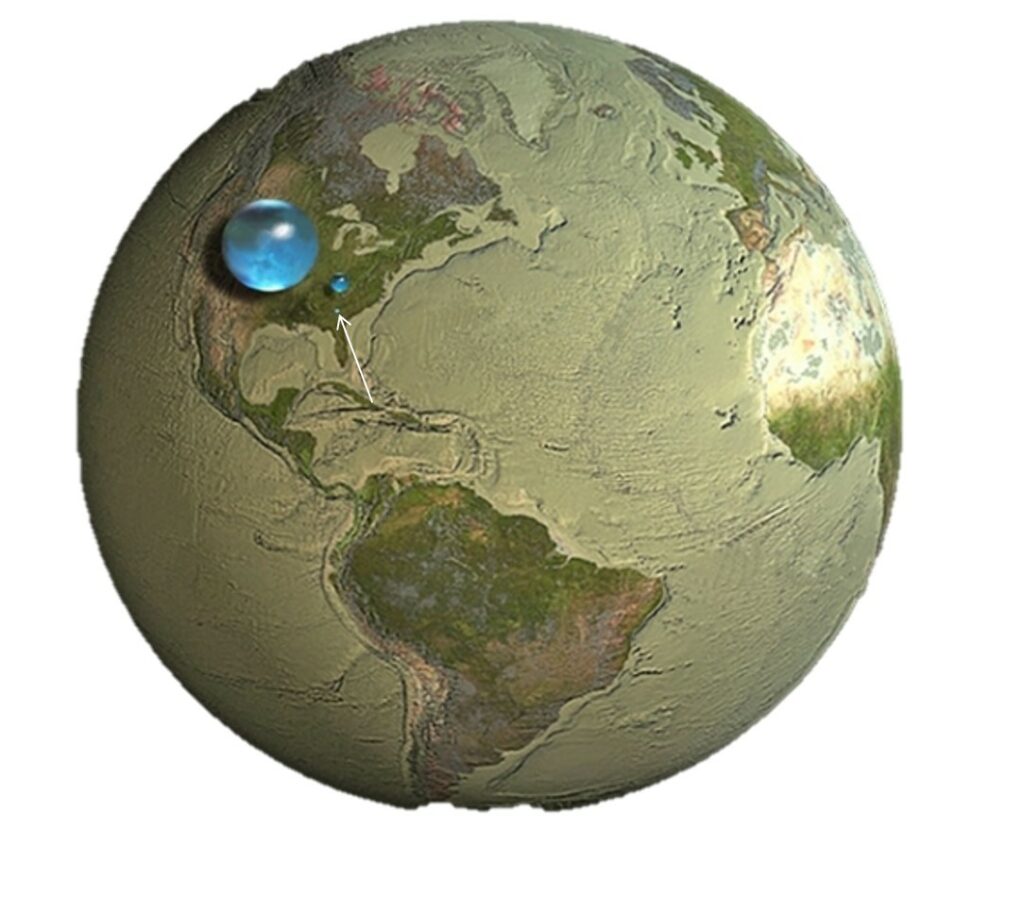
Ziemskie zapasy wody. USGS. Źródło: https://tvnmeteo.tvn24.pl/informacje-pogoda/ciekawostki,49/ile-wody-na-ziemi-mniej-niz-nam-sie-wydaje,48096,1,0.html
Woda i jej własności mogą być inspiracją dla zadań i problemów do rozwiązania na zajęciach z matematyki na różnych poziomach edukacji. Na cząsteczkę wody można spojrzeć z punktu widzenia starożytnej teorii czterech żywiołów, jako na dwudziestościan foremny. Pytanie o ilość kropli w szklance wody dostarczy okazji do obliczeń i szacowania. W świat liczb o zupełnie innym rzędzie wielkości wprowadzi nas pytanie o liczbę cząsteczek wody w jednej szklance.
Zagadki i problemy logiczne są zwykle atrakcyjną dla dzieci formą edukacji, która wzmaga ich ciekawość i kreatywność. Możemy zapytać na przykład, jak sprawdzić czy symetryczna beczka jest napełniona do połowy wodą, czy też jak podzielić 8 litrów wody na połowy mając do dyspozycji pojemniki (niekoniecznie symetryczne) o pojemności 8l, 5l, 3l ?
W literaturze można znaleźć wiele zadań na tak zwaną „przeprawę” albo inaczej „zadania przewozowe”. Jednym z najpopularniejszych i najstarszych zadań tego typu jest zadanie o wilku, kozie i kapuście. Zadanie to znajdowało się już w dziele średniowiecznego anglosaskiego mnicha Alkuina z VIII wieku, a najprawdopodobniej zostało zaczerpnięte z ksiąg jeszcze wcześniejszych. Gospodarz ma do przewiezienia na drugi brzeg rzeki wilka, kozę i kapustę. Dysponuje jednak tak małą łódka, że oprócz niego zmieści się w niej tylko jedno z trojga. Zadanie polega na znalezieniu takiego sposobu przeprawy, by zarówno koza (gdy zostanie na brzegu sam na sam z wilkiem, to źle się to dla niej skończy), jak i kapusta ( może zjeść ją koza) , a także wilk dotarli na drugi brzeg w stanie nienaruszonym. Oczywiście, należy najpierw przeprawić kozę (wilk kapusty nie zje!), następnie wrócić po wilka i przewieźć go na drugą stronę rzeki, a kozę zabrać z powrotem, przewozimy następnie kapustę i na końcu wracamy po kozę i tak mozolna przeprawa dobiega końca. Słynne przeprawowe zadania Alkuina doczekały się bardzo wielu wersji, przykłady można znaleźć np. w Lilavati Szczepana Jeleńskiego [1] lub np. w Internecie http://www.matematyka.wroc.pl/kolkomatematyczne/zadania-przewozowe .
Obliczenia procentowe mogą posłużyć nam do uświadomienia dzieciom znaczenia wody i jej obecności w naszym otoczeniu.
Woda może być tłem zajęć poświęconych geometrii na różnych etapach kształcenia. Geometria płatka śniegu, czyli wody w stałym stanie skupienia może być uzupełnieniem zajęć o własnościach wielokątów foremnych i ich symetrii. Elementy historii matematyki i jej znane problemy można zilustrować słynnym zadaniem o mostach królewieckich.
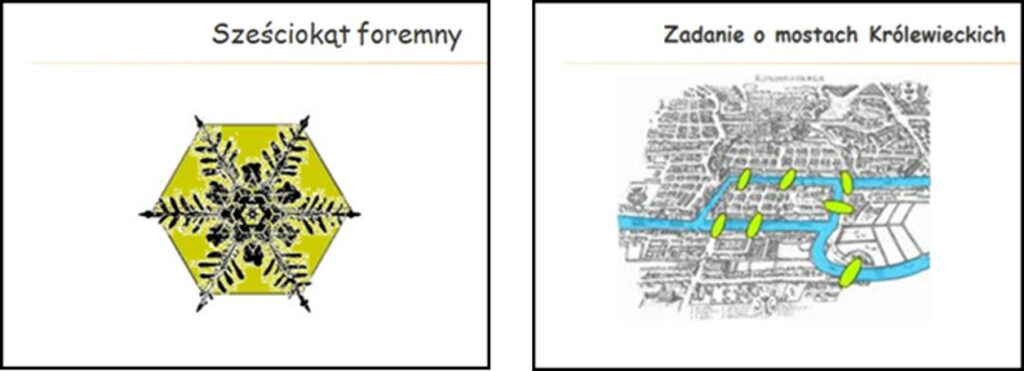
Problem siedmiu mostów dowodzi, że z pozoru błahe pytania, mogą prowadzić do rozwoju nauki. Jak głosi legenda, mieszkańcy Królewca bardzo lubili spacery po swoim pięknym mieście. Przez Królewiec (obecnie Kaliningrad) przepływa rzeka Pregoła w rozwidleniu której znajdują się dwie wyspy. W XVII wieku nad rzeką było 7 mostów (jeden z mostów łączył ze sobą wyspy, pozostałe łączyły wyspy z drugim brzegiem rzeki). Mieszkańców ponoć trapiło pytanie, czy można tak zaplanować wycieczkę, by po wyjściu z domu przejść dokładnie jeden raz przez każdy z mostów i wrócić do domu? Problemem zainteresował się szwajcarski matematyk i fizyk Leonhard Euler, który w 1736 r. udowodnił, że taka wędrówka jest niemożliwa. Praca, w której przedstawił swoje rozważania (Solutio problematis ad geometriam situs pertinentis w Commentarii academiae scientiarum Petropolitanae) dała początek nowego działu matematyki jakim jest teoria grafów , która z kolei przyczynia się do rozwoju informatyki. [2]
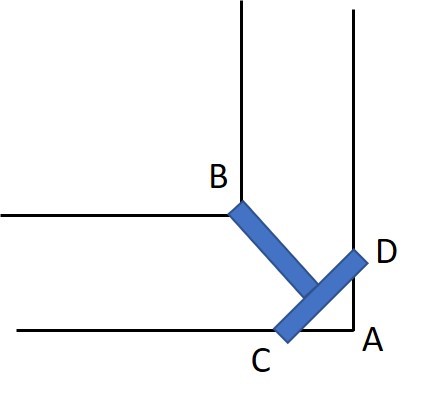
W innym zadaniu przeprawę na drugą stronę rzeki/rowu należy dopiero zbudować. Rów ma stałą szerokość i otacza prostokątne pole. Sprawa nie jest prosta. Do dyspozycji mamy wprawdzie dwie solidne deski, ale ich długość jest równa lub nieznacznie mniejsza niż szerokość rowu i niestety nie mamy żadnych narzędzi. Rysunek przedstawia w jaki sposób za pomocą tych desek zbudować przejście.
Niech szerokość rowu wynosi a, wtedy odcinek AB (przekątna kwadratu o boku a) ma długość 
, a więc około 1,41 razy więcej niż długość naszej deski. Aby „skrócić” tę odległość drugą deskę ustawiamy jak na rysunku. Brzeg deski CD będzie teraz odległy od punktu B o 
, czyli o około 0,914 a. Stąd wniosek, że przy takim ułożeniu desek na oparcie ich na brzegu zostanie około 0,086a, co przy szerokości rowu równej 3 m daje około 25 cm. Dzieci młodsze z powodzeniem mogą rozwiązywać to zadanie praktycznie, posługując się odpowiednim modelem lub rysunkiem na tablicy interaktywnej.
Od kilkunastu lat staramy się pokazywać, że doświadczenia możemy często wykonywać wykorzystując do tego celu przedmioty i materiały codziennego użytku. Prezentujemy także jak może wyglądać współpraca pomiędzy nauczycielami różnych dyscyplin podczas realizacji jednego wybranego zagadnienia. Tym razem przybliżymy zjawisko napięcia powierzchniowego wody. Napięcie powierzchniowe [3] – siły dążące do nadania powierzchni cieczy takiego kształtu, przy którym jej pole powierzchni jest najmniejsze. Wskutek tego powierzchnia cieczy przypomina naciągniętą, sprężystą błonę. Napięcie powierzchniowe jest wynikiem oddziaływań międzycząsteczkowych. Wszystko na temat baniek mydlanych można przeczytać w książce Profesora Krzysztofa Ernsta – Einstein na huśtawce w rozdziale pt. „Tajemnice błon i baniek mydlanych” [4].
Bańki mydlane robiono od czasów, gdy wynaleziono mydło, a więc ich historia liczy prawdopodobnie ponad 4 tysiące lat. Przez stulecia udoskonalano receptury produkcji mydła, a i bańki stawały się coraz bardziej interesujące zachowując oczywiście najbardziej korzystny energetycznie kształt. Figurą geometryczną, która przy największej objętości ma najmniejsze pole powierzchni jest kula, stąd kulisty kształt baniek.
Zapraszamy do zapoznania się z tym zagadnieniem poprzez wykonanie zebranych przez nas doświadczeń.
Doświadczenie 1. Narysowany kwiatek należy wyciąć i zagiąć jego płatki tak, jak zilustrowano na zdjęciu poniżej. Do plastikowego pojemnika wlewamy trochę wody. Na wodzie kładziemy zamknięty kwiatek i obserwujemy co się z nim dzieje?
Napięcie powierzchniowe powoduje utrzymywanie się kwiatka na wodzie, a dzięki zjawisku włoskowatości zaczyna „rozkwitać”.
Doświadczenie 2. Pasek papieru zginamy w taki sposób, żeby można było położyć na nim spinacz. Następnie trzymając za końce papieru kładziemy spinacz na powierzchni wody, a papier ostrożnie wyjmujemy.
Można na powierzchni wody ułożyć więcej spinaczy, wykorzystując do tego celu zamiast paska papieru zwykły widelec. Woda ma „skórę” czyli napięcie powierzchniowe, które pozwala nartnikom biegać po wodzie, a naszemu spinaczowi, mimo że jest metalowy, unosić się na jej powierzchni. Im większa jest powierzchnia styku, tym łatwiej położyć przedmiot na wodzie. W przyrodzie wykorzystują to lilie wodne.
Doświadczenie 3a. Przygotowujemy dwa plastikowe kieliszki. Jeden otwarty, drugi z naklejoną siatką. Każdy napełniamy wodą. Kieliszek bez naklejonej siatki przykrywamy kartką i odwracamy do góry dnem. Robimy to nad tacą lub miską. Woda jest utrzymywana prze kartkę, którą „podpiera” ciśnienie atmosferyczne. Jeśli przesuniemy kartkę, to woda wylewa się z kieliszka. Inaczej jest gdy powtórzymy to doświadczenie z drugim kieliszkiem. Tym razem możemy zabrać kartkę, a woda z kieliszka się nie wyleje. Między włóknami siatki powstają małe kropelki wody utrzymywane przez siły napięcia powierzchniowego. To napięcie powierzchniowe równoważy siłę grawitacji działającą na kropelki wody.
Doświadczenie 3b. Możemy wykonać inną wersję tego doświadczenia i zatkać otwór butelki wypełnionej wodą „korkiem” z sitka do zaparzania herbaty. Butelkę odwracamy wylotem do dołu.
Doświadczenie 4. Na małą podstawkę kładziemy monetę. Następnie za pomocą pipety umieszczamy na powierzchni monety kolejne kropelki wody. Liczymy, po której kropelce woda przeleje się z pieniążka na podstawkę?
Doświadczenie 5a. Z drutu wykonujemy obręcz. Wzdłuż średnicy zawiązujemy nitkę nieco od niej dłuższą. Zanurzamy obręcz w płynie, by powstała na niej cienka błonka cieczy z pływającą w niej nicią. Po przebiciu błony po jednej stronie nitki, nitka przybiera kształt łuku. Doświadczenie możemy zmodyfikować i końce nitki zbliżyć do siebie tak, by powstała pętelka. Po przebiciu błony wewnątrz pętelki nitka przyjmuje kształt okręgu.
Doświadczenie 5b. Jakie możliwości posiada napięcie powierzchniowe można pokazać mocując nitkę na rurce do picia napojów, tak jak pokazuje fotografia. Zwisającą nitkę obciążamy spinaczem. Cały zestaw zanurzamy w płynie do robienia baniek. Po wyjęciu z płynu widzimy, że błona, która powstała pomiędzy nitkami spowodowała, że przyjęły one kształt łuku.
Doświadczenie 5c. Z rurek do picia napojów wykonujemy ramkę, którą zanurzamy w mydlanym płynie. Następnie kawałek prostej rurki kładziemy na wierzch ramki i przebijamy błonę, po prawej stronie położonej na ramce rurki. Druga część błony po lewej stronie rurki zacznie ściągać rurkę do lewej krawędzi ramki.
Doświadczenie 6. Na stole kładziemy dwie kolorowe, zalaminowane kartki. Jedną smarujemy płynem do mycia naczyń, drugą oliwą. Na każdej z kartek umieszczamy za pomocą pipety dużą kroplę wody i obserwujemy jak każda z nich się zachowuje? Na kartce posmarowanej oliwą woda przyjmuje kształt kulisty, a na posmarowanej płynem do naczyń rozpływa się. Dzieje się tak dlatego, że na kartce pokrytej oliwą siły spójności (działające między cząsteczkami wody) są większe od sił przylegania działającymi między wodą, a natłuszczoną kartką. W przypadku drugiej kartki jest odwrotnie.
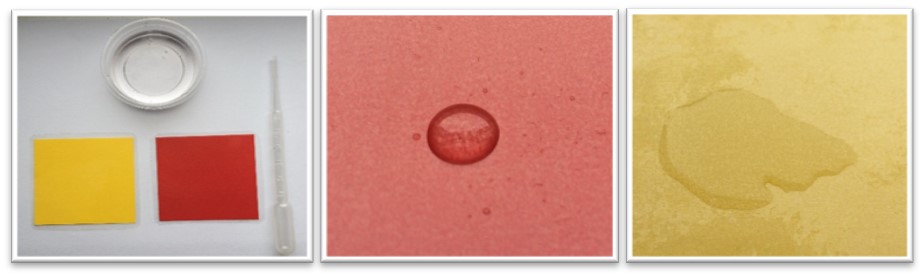
To ma związek z dwoma powiedzeniami: „Spływa jak woda po kaczce” i „Wygląda jak zmokła kura”
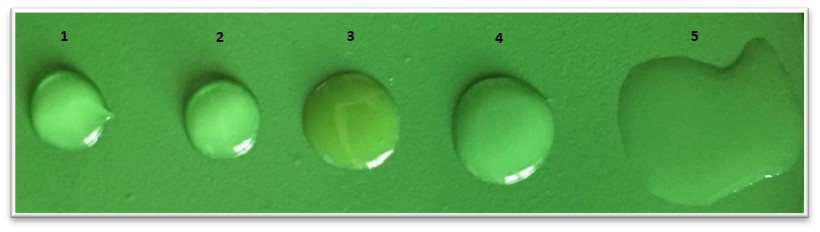
Doświadczenie 7. Na zalaminowanej kartce papieru umieszczamy krople różnych substancji, których wartości napięcia powierzchniowego można odczytać z tabeli. Porównujemy zachowanie się kropel tych substancji, umieszczonych na tej samej kartce. Obserwujemy, że im mniejsze jest napięcie powierzchniowe cieczy, tym bardziej rozlewa się na kartce.
| Napięcie powierzchniowe substancji σ ·10 -3 [N/m] w temp. 20 oC | ||
| 1. | woda | 72,8 |
| 2. | gliceryna | 59,4 |
| 3. | olej | 33,0 |
| 4. | alkohol metylowy | 22,6 |
| 5. | woda z płynem do naczyń | 10,0 |
Doświadczenie 8. Do pojemnika wypełnionego wodą wsypujemy dwie, trzy szczypty maku. Następnie zanurzamy koniec patyczka do czyszczenia ucha w płynie do mycia naczyń i umieszczamy go w środku pływającego po wodzie maku.
Mak „ucieknie” w stronę zewnętrznych ścianek naczynia, ponieważ płyn do mycia naczyń znajdujący się na końcu patyczka zmniejszył napięcie powierzchniowe wody.
Doświadczenie 9a. Do plastikowego talerzyka nalewamy odrobinę mleka 3,2% tłuszczu, wsypujemy na powierzchnię mleka (w różnych miejscach) kolorowe barwniki do barwienia jaj. Następnie zanurzamy w kilku miejscach patyczek nasączony płynem do mycia naczyń. Barwniki zaczynają się mieszać, tworząc kolorową mozaikę na mleku.
Doświadczenie 9b. Do plastikowego talerzyka nalewamy tak jak w poprzednim doświadczeniu odrobinę mleka 3,2% tłuszczu. Tym razem wkraplamy do mleka (w różnych miejscach) po kilka kropelek różnobarwnych atramentów. Zamiast atramentu można wykorzystać rozpuszczone w małej ilości wody barwniki do jaj. Następnie zanurzamy w kilku miejscach patyczek nasączony płynem do mycia naczyń. Barwniki zaczynają się mieszać, tworząc kolorową mozaikę na mleku.
Mleko zawiera tłuszcz, zatem zabarwione kropelki wody nie mieszają się z nim. Wkraplając do mleka detergent, osłabiamy napięcie powierzchniowe powodując, że zabarwione kropelki mogą się rozpływać.
Zapraszamy także do obejrzenia filmu na kanale „KiteLab” Edyty Dzikowskiej.
Doświadczenie 10. Wyciętą z grubego papieru „rybkę” (na zajęciach wykorzystujemy rybki wykonane na drukarce 3D) umieszczamy na powierzchni wody. Następnie w otworek wycięty na środku rybki wlewamy kroplę płynu do mycia naczyń. Rybka zaczyna odpływać z tego samego powodu, co mak w poprzednim doświadczeniu. Warto omawiając sposoby zmniejszania napięcia powierzchniowego wykorzystać na zajęciach opowiadania Włodzimierza Wajnerta „Zacieki” oraz Jerzego Wójciaka „Kłopoty nartnika” [5] i [6].
Doświadczenie 11. Wykorzystując pojemnik z płynem do robienia baniek, wykonujemy dużą bańkę mydlaną, a następnie próbujemy ją odbić jak piłkę, dłonią ubraną w materiałową rękawiczkę. Nie odbijemy bańki gołą ręką, bo przyklei się ona do ręki i pęknie.
Doświadczenie 12. Na środku przezroczystego arkusza plastikowej folii formatu A4 umieszczamy trochę płynu do robienia baniek mydlanych. Do tego płynu wkładamy jeden koniec rurki do picia napojów, a drugi koniec do ust, wydmuchując bańkę. Następnie wyjmujemy rurkę, ponownie zanurzamy ją w płynie do robienia baniek, wkładamy ją do zrobionej poprzednio bańki. W środku już istniejącej bańki wydmuchujemy następną. Czynność tę powtarzamy kilka razy, otrzymując w ten sposób bańki w bańkach.
Doświadczenie 13. Na szklaną rurkę w kształcie litery Y lub T nakładamy krótkie gumowe wężyki lub plastikowe przeźroczyste rurki , które można kupić na stoiskach ogrodniczych. Dwa końce rurki zanurzamy w płynie do robienia baniek, trzeci umieszczamy w ustach i wydmuchujemy bańki. Następnie jeden z wężyków zaciskamy, w drugi dalej wdmuchujemy powietrze, żeby jedna z baniek była większa. Otrzymujemy dwie bańki o różnych średnicach, jeśli zatkamy przewód przez który wdmuchiwaliśmy powietrze. Po jego otwarciu duża bańka wchłonie małą, ponieważ zakrzywiona błonka wywiera ciśnienie odwrotnie proporcjonalne do promienia krzywizny bańki skierowane do jej wnętrza. [7]
Czy bańki mydlane zawsze są przeźroczyste?
Doświadczenie 14. Najczęściej wypełniamy bańki mydlane powietrzem, co powoduje, że są przezroczyste. Jeśli chcemy otrzymać bańki nieprzeźroczyste, to możemy do tego celu wykorzystać nawilżacz powietrza. Przymocowujemy do jego wylotu kawałek plastikowego węża, którego drugi koniec zanurzamy na chwilę w płynie do robienia baniek i włączamy nawilżacz do prądu. Po chwili powstają piękne bańki.
Podobny efekt uzyskamy gdy zastosujemy wytwornicę dymu. Napełniamy dymem rurę PCV. Jeden koniec rury zanurzamy w płynie do robienia baniek, a drugi przykładamy do ust i wydmuchujemy bańki.
Czy bańki mydlane zawsze mają kształt kulisty?
Doświadczenie 15. Do pojemnika wlewamy płyn do robienia baniek mydlanych i wkładamy dwie rurki do napojów połączone sznurkiem. Namoczone, złączone rurki wyjmujemy z płynu i powoli je rozdzielamy. Między rurkami i sznurkami powstanie piękna, kolorowa mydlana „szyba”. Możemy zrobić dużą szybę wykorzystując zamiast rurek, dwie drewniane listewki.
Doświadczenie 16. W płaskim pojemniku z płynem do robienia baniek umieszczamy podstawkę, na której stawiamy zabawkę lub dziecko (jeśli pojemnik jest odpowiednich rozmiarów). Następnie zanurzamy w płynie obręcz i podnosimy ją do góry tworząc cylinder z mydlanej błony, w którym zamknięta zostaje zabawka lub osoba.
Doświadczenie 17. W płynie do mycia naczyń zanurzamy szkielety różnych brył wykonanych z rurek do picia zimnych napojów. Błony powstające na różnych szkieletach brył przyjmują specyficzne kształty, minimalizujące wielkość powierzchni.
Kolejny film z kanału „KiteLab Experiments” Edyty Dzikowskiej.
Fizyka baniek i akwagrafia…
Doświadczenie 18. Płyn do mycia naczyń mieszamy z kolorowym tuszem. Następnie całą zawartość wlewamy do płaskiego pojemnika (miski, kuwety lub dużej podstawki do kwiatów) i za pomocą rurki do picia napojów robimy kolorowe bańki mydlane. Do tych baniek przykładamy kartkę białego papieru tak, żeby pękające bańki pozostawiły ślad na papierze. Otrzymujemy piękną grafikę, którą używając wyobraźni, oraz kredki lub pisaka zamieniamy w dzieło sztuki. Doświadczenie możemy powtórzyć z innym kolorami tuszu.
Doświadczenie 19. Dreszczyku emocji mogą dostarczyć płonące bańki mydlane. Do miski wlewamy płyn do robienia baniek i zanurzamy w nim pojemnik z gazem do zapalniczek, zaworem do dołu. Naciskając zanurzony w płynie zawór wytwarzamy przeźroczyste bańki wypełnione butanem. Następnie zbieramy bańki na rękę i podpalamy długą zapalniczką, poruszając ręką, żeby się nie poparzyć. Doświadczenie wykonuje osoba dorosła!
Doświadczenie 20. Niesamowite bańki można stworzyć w czasie mroźnej zimy. Nam nie udało się zrobić tak pięknych zdjęć, bo przez kilka ostatnich lat w Opolu nie było mroźnej zimy. Załączamy zdjęcia ze strony pixabay, zezwalającej na wykorzystywanie ich zdjęć.
pixabay.com/pl/photos/bańki-mydlane-zimno-zima-mydło-2182943/
pixabay.com/pl/images/search/mróz%20bańka/
pixabay.com/pl/photos/bańka-mydlana-matowe-zima-zimno-2000295/
Warto także zobaczyć „KiteLab Experiments” Edyty Dzikowskiej.
Bańka mydlana
Gdy wydmuchujemy bańkę mydlaną, początkowo jest ona bezbarwna. Gdy błona staje się dostatecznie cienka, pojawiają się barwy. Jest to wynik interferencji światła w cienkich warstwach. Więcej na ten temat można przeczytać we wspomnianej wyżej książce Krzysztofa Ernsta [2].
Kilka przepisów na bańki mydlane. W przepisach używamy wody destylowanej, która nie ma żadnych zabrudzeń, płynu do mycia naczyń bez dodatku balsamu, zmniejszającego napięcie powierzchniowe wody oraz gliceryny sprawiającej, że banki są bardziej sprężyste i wytrzymalsze. Można je wtedy odbijać. Jeśli chcemy wykonać ogromne bańki mydlane, to musimy roztwór zagęścić mąką kukurydzianą. Trzeba także zwracać uwagę na to, czy dysponujemy zwykłym płynem czy koncentratem? Przygotowanie roztworu tylko z płynu i wody pozwala nam stworzyć małe bańki żyjące krótko. Dodanie do roztworu gliceryny, zapobiega szybkiemu odparowaniu wody i znacznie wydłuża ich czas życia. Gliceryna pozostawia jednak ślady. Zatem wybór przepisu zależy od tego, gdzie robimy doświadczenia i jaki chcemy osiągnąć efekt.
Przepis 1. 6 porcji wody, 3 porcje przezroczystego płynu do mycia naczyń, 1 porcja gliceryny.
Przepis 2. (Hiszpania – Anton Aubanell) 50% woda, 40% płyn do naczyń, 10% gliceryna.
Przepis 3. (bańki z cukrem, bez gliceryny, która zostawia plamy) – 250 ml przegotowanej lub destylowanej wody, 3 łyżeczki oleju, 4 łyżeczki cukru, 6 łyżeczek płynu do naczyń jeśli bańki będą pękać to dodajemy więcej płynu do naczyń.
Przepis 4. (na wielkie bańki – Czechy – Věra Pejčochová) – (porcja to 250 ml) 12 porcji wody, 1 porcja płynu, 1 porcja kukurydzianej mąki, 2 łyżki proszku do pieczenia. Roztwór musi poleżeć. Przed użyciem wymieszać, żeby mąka nie osiadła na dnie. Jeśli bańki pękają, trzeba dodać więcej płynu do naczyń.
Wielkie bańki mydlane na kanale „KiteLab Experiments” Edyty Dzikowskiej.
Bibliografia:
[1]. Szczepan Jeleński ; Lilavati Państwowe Zakłady Wydawnictw Szkolnych, Warszawa 1968
[2]. Mioduszewski J.; Mosty Królewieckie dwieście lat później. Delta 4 (1981)
[3]. Hewitt P.; Fizyka wokół nas, Wydawnictwa Naukowe, Warszawa 2000, s. 226-228, s.527
[4].Ernst K; Einstein na huśtawce czyli fizyka, zabaw, gier i zabawek, „Tajemnice błon i baniek mydlanych”, Prószyński i S – ka, Warszawa 2002, s.145-155
[5]. Wajnert W.; Przygody z Machefim, Zacieki”, Wydawnictwo Czasopism i Książek technicznych NOT-Sigma, Warszawa 1987, s. 27-29
[6]. Wójciak J; Ćwiczenia dla detektywów przyrody, Polska Oficyna Nauczycielska, Wrocław 1995, s. 62-63
[7]. Domański J.; Mazur B.; Fizyka wokół nas, Doświadczenia pokazowe- poradnik dla nauczycieli gimnazjum i liceum, Wydawnictwo Respolona, Łódź, s. 45
www.em.muni.cz/vite/5596-badatelna-13-dil-proc-drzi-sponky-na-hladin
www.em.muni.cz/vite/6068-badatelna-16-dil-jak-foukat-velke-bubliny
www.matematyka.wroc.pl/kolkomatematyczne/zadania-przewozowe.
Zdjęcia i rysunki: Zbiory własne
Autorki: Irena Juńczyk – chemia, Aleksandra Opaska – matematyka, Krystyna Raczkowska-Tomczak – fizyka – Opole, Věra Pejčochová – matematyka, fizyka – Brno
Publikowane: Raczkowska-Tomczak Krystyna; Juńczyk Irena.; Opaska Aleksandra; Pejčochová Vera.; Biuletyn Polskiego Stowarzyszenia Nauczycieli Przedmiotów Przyrodniczych „Woda pod napięciem”, Nauczanie Przedmiotów Przyrodniczych, tom 68, 2/2019, Toruń 2019, s.22-30