Lustrzane odbicia wokół nas. Symetria i sztuka. O lustrzanych literach, piśmie i palindromach. Szyfry i magiczne sztuczki z symetrią w tle.
„Są dwa główne powody utraty matematycznego wątku: za dużo formalnych reguł, za mało zdrowego rozsądku” – ta parafraza słów Jerzego Paczkowskiego jest mottem książki Danuty Zaremby o nauczaniu matematyki i jest też zasadą, którą kierujemy się w czasie zajęć z matematyki w Centrum Nauk Przyrodniczych. Należy bowiem pamiętać, że zrazić dzieci do matematyki jest bardzo łatwo. Sprzyja temu postawa wielu dorosłych i wciąż popularne przekonanie, że matematyka jest dla wybranych, a humanistom nie jest do niczego potrzebna. Tymczasem logika podpowiada, że „Jeśli nie umiesz matematyki, nie oznacza to, że jesteś humanistą. Oznacza, że nie umiesz matematyki” (Marcin Jakubowski https://twitter.com/jakmarcin/status/5636907250289377290).
Celem prowadzonych zajęć jest między innymi pokazanie, że matematyka jest wokół nas, towarzyszy nam na co dzień i nie powinna być traktowana jako zło konieczne. Warto bowiem pamiętać, że „żaden kraj z ambicjami nie może być krajem analfabetów matematycznych” (Immanuel Kant).
„Symetryczne znaczy piękne” to przykład tematu, który bazuje na doświadczeniach każdego z nas. W potocznym słowa znaczeniu symetrię utożsamiamy z harmonią, ładem i uporządkowaniem. Lubimy symetrię, bo wnosi ona w nasze życie właściwe proporcje i jest nam znana z otoczenia. Matematyczne znaczenie słowa symetria różni się od potocznego i jest dużo szersze. Celem zajęć nie jest jednak sformalizowanie wiadomości dotyczących symetrii, ale intuicyjne badanie jej własności. Język i ćwiczenia muszą być dostosowane do wieku i indywidualnych możliwości uczestników zajęć. Niektóre z proponowanych ćwiczeń realizowane były na zajęciach otwartych dla dzieci młodszych (5 – 10 lat) , w Zespole Szkół Specjalnych , a inne na zajęciach dla dzieci starszych (starsze klasy szkół podstawowych i klasy gimnazjalne).
- Symetria osiowa (lustrzana).
Proponowane ćwiczenia powinny doprowadzić do intuicyjnej odpowiedzi na pytania: kiedy figury są symetryczne (lustrzane) i jakie mają własności.
O figurach, które są swoimi lustrzanymi odbiciami mówimy, ze są do siebie symetryczne względem linii ustawienia lusterka (osi symetrii).
Punkty symetryczne względem prostej są równo od niej oddalone, leżą na prostej prostopadłej do osi symetrii i po jej przeciwnych stronach.
Ćwiczenie 1. Dzieci oglądają swój obraz w lustrze, obserwują jak zachowuje się ich odbicie, gdy np. podnoszą lewą rękę, prawą nogę, itp.
Ćwiczenie 2. Dzieci stają w dwóch rzędach naprzeciwko siebie.
Jeden rząd to „eksperymentatorzy”, drugi to „odbicia lustrzane”. „Eksperymentatorzy” wykonują różne, proste ruchy, a zadaniem „odbić” jest skopiowanie ich ruchów tak, jak zrobiłoby to lustro.
Dzieci mogą też obejrzeć slajdy i na ich podstawie opowiedzieć jak wyglądają i jak są położone „lustrzane” obrazy.


Fot.1.aanais.bnaughty
Fot.2 https://commons.wikimedia.org/wiki/File:Kitten_and_partial_reflection_in_mirror.jpg
Ćwiczenie 3. Uczniowie obserwują jak wyglądają odbicia w lusterkach różnych narysowanych postaci i przedmiotów, a następnie decydują, czy wyświetlane na tablicy rysunki są, czy nie są „lustrzane” ? Swoje odpowiedzi uzasadniają, a w przypadku, gdy rysunki są symetryczne („lustrzane”), decydują gdzie należy dorysować oś symetrii (linię lustra).

Ćwiczenie 4. Na tablicy interaktywnej i na kartach pracy dzieci uzupełniają rysunki tak, aby kształty były symetryczne względem zadanej osi symetrii.

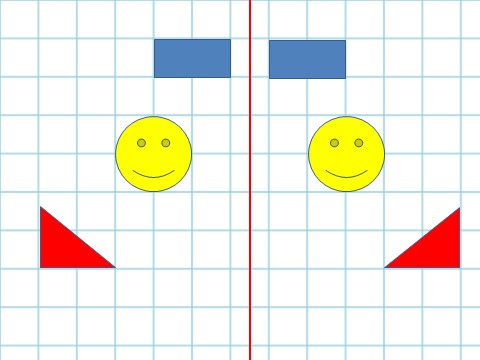
2. „Osiowosymetryczne” czyli … atrakcyjne.
Prosta względem której figura jest symetryczna sama do siebie to oś symetrii tej figury. Figury, które mają oś symetrii nazywamy osiowosymetrycznymi.
Symetria i łamanie symetrii to zjawisko powszechne. Jeżeli spojrzymy wokół siebie bez trudu dostrzeżemy te dwa zjawiska. Jedna połowa liścia jest lustrzanym odbiciem drugiej, symetryczna jest zewnętrzna budowa zwierząt, większość produktów naszej cywilizacji jest też symetryczna.
W świecie zwierząt symetria jest wizytówką zdrowia i atrakcyjności. Wybierając partnera pani jaskółka zwraca uwagę na symetrię ogonka kandydata, symetryczne poroże jeleni, saren czy reniferów świadczy o wartości ich genów. Nie inaczej jest u ludzi. Symetryczna, owalna twarz uważana jest za idealną, a starożytni Grecy uważali, że symetria twarzy świadczy o większej zdolności umysłowej. Tymczasem niewielka asymetria twarzy jest normą, co łatwo zauważyć robiąc odpowiednie zdjęcia.
Ćwiczenie 5. Dzieci podają różne przykłady przedmiotów i elementów przyrody osiowosymetrycznych. Wskazują, gdzie znajduje się ich oś symetrii , czyli własne wewnętrzne lusterko jak określił oś symetrii jeden z uczestników zajęć.


Ćwiczenie 6. Wykonujemy zdjęcia twarzy dzieci en face. Po podzieleniu zdjęcia na polowy i odbiciu lustrzanym każdej z połówek otrzymujemy dwie różniące się twarze. Dzieciom tak wykonane „portrety” bardzo się podobają, a dla rodziców stanowią duże zaskoczenie.



To jest Agnieszka To jest Agnieszka „prawostronna” To jest Agnieszka „lewostronna”
Dlaczego rysując trójkąt albo czworokąt najczęściej wychodzi nam trójkąt równoboczny i kwadrat?
Te figury wizualnie wydają się nam bardziej przyjazne i atrakcyjne ze względu na ich symetryczność.
Ćwiczenie 7. Dzieci szukają osi symetrii figur geometrycznych poprzez składanie wyciętych z papieru modeli tak, aby obie części figury idealnie się na siebie nałożyły.
3. Symetryczne znaczy piękne.
Symetria to jeden z najstarszych sposobów tworzenia sztuki. Najprostszym dziełem sztuki może być obrazek z kolorowych kleksów podwojonych symetrycznie przez złożenie kartki papieru. Chociaż piękno jest czymś subiektywnym i nieuchwytnym, to większość osób za ładniejsze uznaje to, co symetryczne. Natura przyzwyczaiła nas do symetrii, a to co znajome wydaje się nam bardziej atrakcyjne. Symetryczne wytwory naszej cywilizacji mają zwykle oś pionową zgodnie z naturą i działającą powszechnie grawitacją (z góry na dół).

Ćwiczenie 8. Proponujemy uczestnikom zajęć stworzenie własnych, symetrycznych dzieł. Mogą to być wycinanki uzyskane przez nacinanie odpowiednio złożonego papieru. W zimie można tworzyć na bazie sześciokątów foremnych śnieżynki lub symetrycznie ozdabiać symetryczne choinki.

4. Punkt rządzi!, czyli o symetrii środkowej.
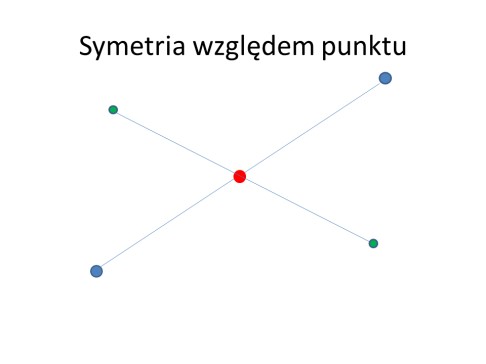
Symetria środkowa względem punktu S to takie przekształcenie, w którym obrazem dowolnego punktu A płaszczyzny jest punkt A1 taki, że S jest środkiem odcinka AA1.
Symetria środkowa na płaszczyźnie jest złożeniem dwóch symetrii osiowych o osiach przecinających się w środku symetrii pod kątem prostym.
W jaki sposób „działa” symetria względem punktu można zilustrować zabawą, gdzie punkty płaszczyzny to dzieci, środek symetrii S, który „rządzi” dziećmi to wolontariusz, a odcinki łączące punkty z ich obrazami to sznurki.

Można również przygotować animację ilustrującą to przekształcenie:

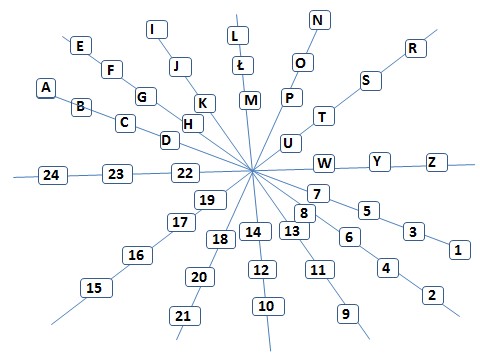
Ćwiczenie 9. Uczestnicy zajęć otrzymują kartę szyfrów. Ich zadaniem jest zaszyfrowanie np. swojego imienia, a także rozszyfrowywanie otrzymanych wiadomości.
Starsi uczniowie mogą otrzymać tylko kartę kodów i wiadomość do rozszyfrowania. Odkrycie jak działa szyfr pozostaje do odkrycia.

5. O palindromach i liczbach biegnących z powrotem. Symetryczność dotyczy nie tylko obiektów matematycznych. Litery ustawione symetrycznie tworzą wyrazy, które można czytać nie tylko od strony lewej do prawej, ale i od prawej do lewej. Można układać całe zdania, które można czytać w zwykły sposób jak i wspak. Takie zdania to palindromy. Ponoć pierwsze słowa wypowiedziane przez człowieka były palindromem. Adam przywitał Ewę w raju, mówiąc: Madam, I’m Adam. Tradycja tych słownych zabaw sięga starożytności. Palindromy tworzyli starożytni Grecy, Rzymianie i Egipcjanie. Być może, stosowano je jako rodzaj szyfru czy magii. Tworzeniem takich, często zabawnych zdań, zajmowali się w Polsce miedzy innymi: Julian Tuwim („Popija rum as, samuraj i pop”), Edmund John i inni. Obecnie czołowym twórcą palindromów jest Tadeusz Morawski, profesor elektroniki popularyzujący sztukę układania i historię polskich palindromów. W roku 2007 Tadeusz Morawski utworzył Muzeum Palindromów w Nowej Wsi koło Serocka.
Ćwiczenie 10. Ułożyć dowolny palindrom złożony z jednego, dwóch, … wyrazów
Układanie palindromów słownych może być dla dzieci zabawą, ale palindromy liczbowe mogą być już pretekstem do rozwiązywania problemów.
Liczba palindromiczna to taka, która czytana od lewej strony do prawej jak i odwrotnie, jest taka sama.
Przykładów palindromów liczbowych jest oczywiście nieskończenie wiele np. 11211, 1234554321
Ćwiczenie 11. Wypisać wszystkie palindromy dwucyfrowe. Ile ich jest? Odp:(11, 22, …, 99)
Ile jest palindromów trzycyfrowych?
Ile jest palindromów czterocyfrowych?
Uczniowie starsi mogą próbować swoją odpowiedź uogólnić dla palindromu n – cyfrowego
Każdy z dziewięciu palindromów dwucyfrowych można zamienić na trzycyfrowy wstawiając w środek kolejne cyfry: 1,2, …9, a więc na dziesięć sposobów. Na przykład w palindromie 11 pomiędzy jedynki wstawiamy kolejno cyfry 1, 2, 3, 4, 5, … , otrzymując 111,121,131,141,151, …. Podobnie postępujemy z pozostałymi ośmioma palindromami dwucyfrowymi. Stąd trzycyfrowych palindromów będzie 90.
Z kolei, aby z trzycyfrowego uzyskać czterocyfrowy, musimy powtórzyć „środkową” cyfrę, a to znaczy, że każdemu palindromowi złożonemu z trzech cyfr odpowiada jeden złożony z czterech. Na przykład palindromowi 111 będzie odpowiadał czterocyfrowy 1111, trzycyfrowemu 121 czterocyfrowy 1221, trzycyfrowemu 131 – czterocyfrowy 1331 i tak dalej.
6. Jeszcze trochę symetrii.
Znając już własności figur symetrycznych można zastosować tę wiedzę zarówno w celach czysto praktycznych , jak i rozrywkowych.
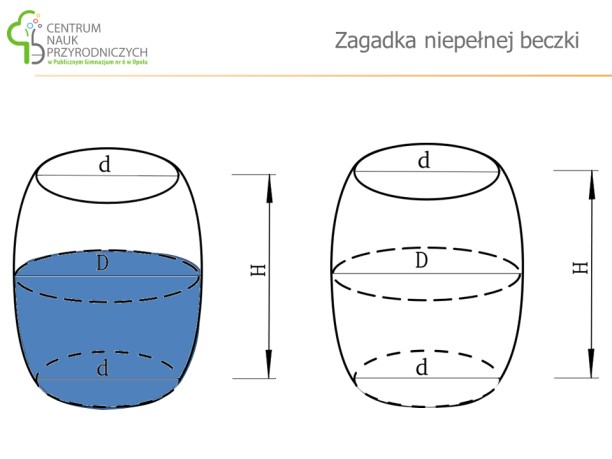
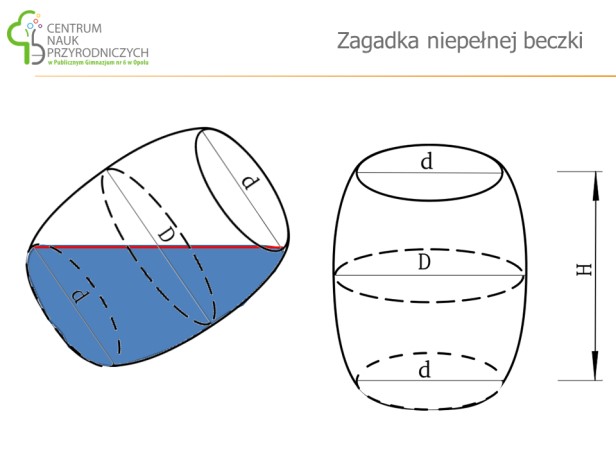
Ćwiczenie 12. Jak sprawdzić, bez żadnych pomocy i przyrządów, czy pojemnik jest napełniony wodą w połowie, czy też wody jest mniej, czy więcej, niż połowa objętości?
Jeśli żaden z uczestników nie poda poprawnego rozwiązania, proponujemy obserwowanie jak powoli wylewamy wodę z naszego pojemnika. Czy ten sposób jest dobry dla dowolnego pojemnika?
Przy okazji realizowania w CNP innych tematów z matematyki również wykorzystywane są własności symetrii. Symetria kart stanowi podstawę sztuczki karcianej na zajęciach „James Bond i matematyka”[8]. Jak grać, żeby wygrać? Wygraną w grze geometrycznej, której opis można znaleźć w „Lilavati” Szczepana Jeleńskiego[4] str. 104, zapewnia znajomość własności symetrii środkowej.
Symetrie występują nie tylko w wielu działach matematyki. Odgrywają ogromną rolę w fizyce, biologii, chemii. „Prawa natury” okazują się bowiem niezwykle symetryczne. Piękno i uniwersalność symetrii zauważali filozofowie i naukowcy już od starożytności. Współcześnie nie sposób przecenić ich znaczenia. Brian Greene amerykański profesor fizyki i matematyki powiedział „ Ze współczesnej perspektywy symetrie są dla nas podstawą , z której wynikają prawa natury”. Z naszej skromnej szkolnej perspektywy symetrie mogą być sposobem na zainteresowanie dzieci otaczającym nas światem.
Bibliografia:
[1] Ian Stewart , „Gabinet matematycznych zagadek”. Wydawnictwo Literackie
[2] Krzysztof Ciesielski, Zdzisław Pogoda, „Królowa bez Nobla. Demart SA, Warszawa 2013
[3] Władysław Kopaliński, „Koty w worku, czyli z dziejów pojęć i rzeczy. Oficyna Wydawnicza Rytm
[4] Szczepan Jeleński, „Lilavati”. Wydawnictwa Szkolne i Pedagogiczne, 1968
[5] http://www.swiatnauki.pl/8,1456.html
[6]https://books.google.pl/books?id=K90yU7i1y_YC&pg=PA39&lpg=PA39&dq=symetria+praw+natury&source=bl&ots=9tMEsOTnZd&sig=4p7caeHkxn1L6hPPTKGEKgv035o&hl=pl&sa=X&ved=0ahUKEwiWrqnvgqbQAhWmIcAKHf-uCKMQ6AEIJzAC#v=onepage&q=symetria%20praw%20natury&f=false
[7] https://pl.wikipedia.org/wiki/Palindrom
[8] Bujak B. Ociepa M. Opaska A. Raczkowska-Tomczak K. Tomalak A.; Biuletyn Polskiego Stowarzyszenia Nauczycieli Przedmiotów Przyrodniczych; „I am Bond, Science Bond…”, Nauczanie Przedmiotów Przyrodniczych, 2/2013, Toruń 2013, s.30-39
[9] https://wszystkoconajwazniejsze.pl/maria-wanke-jerie-dekalog-nauczania-matematyki/
Zdjęcia: https://pixabay.com/pl/photos/architektura-perspektywiczny-budynek-828596/
Dziękujemy Agnieszce za użyczenie nam swojego wizerunku.
Autor: Aleksandra Opaska
Publikowane: Opaska A.; Biuletyn Polskiego Stowarzyszenia Nauczycieli Przedmiotów Przyrodniczych , „Symetryczne znaczy piękne”, Nauczanie Przedmiotów Przyrodniczych, 3/2016, Toruń 2016, s.36-41
Drugą częścią zajęć są zajęcia z fizyki pt. „Po drugiej stronie lustra” Krystyny Raczkowskiej-Tomczak
