„Matematyka w jaskini hazardu”, czyli – zawsze masz szansę, zwodnicze kostki, karty, zakłady, losowania i inne zagadki…
Co wspólnego może mieć agent Jej królewskiej Mości z matematyką? Przystojny, błyskotliwy, o niezliczonych talentach bywalec światowych salonów i matematyka! Pomysłów, by postać agenta 007 była pretekstem do rozważań matematycznych może być jednak wiele. Można zaproponować uczniom tematy z różnych działów matematyki i na różnych poziomach kształcenia.
Całość opracowania pt. ”I am Bond” to kwartet stworzony przez matematykę, fizykę chemię i biologię. Zapraszamy do lektury wszystkich części.
1. Własności liczb
Rozważania można rozpocząć od pseudonimu: 007. Mamy liczbę! A wiec coś, co każdemu kojarzy się z matematyką. Wszak już od Pitagorasa „Liczby rządzą światem”, a „ Liczba jest istotą rzeczy”. Można rozważać własności i historię liczby zero, ale można zająć się również liczbą 7. SIEDEM to liczba w wielu kulturach uważana za mistyczną,
wyróżniającą się bogatą symboliką. W wielu mitologiach i religiach świata była atrybutem bogów, symbolem całości, dopełnienia, symbolizowała związek czasu i przestrzeni. Siódemka pojawiała się w architekturze, świętych pismach i kosmologii. Bywa szczęśliwą, cudowną (siedem cudów świata), kojarzy się miedzy innymi z siedmioma dniami tygodnia czy siedmioma grzechami głównymi.

Ze szkoły podstawowej uczniowie znają cechy podzielności przez 2, 3, 4 , 5 , 6, 8, 9. A co z dzieleniem przez 7? Nie ma cechy podzielności przez siedem? Oczywiście jest, i to nie jedna.
Cecha podzielności przez 7
Metoda I
Dzielimy liczbę na trzycyfrowe grupy cyfr począwszy od prawej strony. Obliczamy sumę różnic liczb utworzonych w następujący sposób: od liczby utworzonej przez trzy ostatnie cyfry odejmujemy liczbę utworzoną przez poprzedzające ją trzy cyfry. Jeżeli tak utworzona suma jest podzielna przez 7, to liczba dzieli się przez 7.
Przykład:
Weźmy liczbę 2233445566. Dzielimy ją na grupy cyfr : 2 233 445 566.
Tworzymy różnice: 566 – 445 = 121 oraz 233 – 2 = 231
Obliczamy sumę różnic: 121 + 231 = 352. 352 nie jest podzielna przez 7, więc liczba 2233445566 nie dzieli się przez 7.
Metoda II
Oddzielamy dwie ostatnie cyfry tej liczby i z tak powstałej liczby dwucyfrowej obliczamy resztę z dzielenia przez 7. Liczbę powstałą z pozostałych cyfr podwajamy i postępujemy z nią jak poprzednio. Czynność powtarzamy tak długo, aż wyczerpiemy wszystkie cyfry liczby. Wówczas sumujemy wszystkie powstałe reszty. Jeśli suma reszt jest podzielna przez 7, to także liczba wyjściowa jest podzielna przez 7.
Przykład:
Weźmy liczbę 86419746. Oddzielamy dwie ostatnie cyfry 46 i obliczamy resztę z dzielenia 46 przez 7:
46 : 7 = 6 reszta = 4
Czynność powtarzamy do wyczerpania się cyfr:
2 ∙ 864197 = 1728394 94 : 7 = 13 reszta = 3
2 ∙ 17283 = 34566 66 : 7 = 9 reszta = 3
2 ∙ 345 = 690 90 : 7 = 12 reszta = 6
2 ∙ 6 = 12 12 : 7 = 1 reszta = 5
Obliczamy sumę reszt:4 + 3 + 3 + 5 + 6 = 21. Liczba 21 dzieli się przez 7, to 86419746 też jest podzielna przez 7.
Czary liczby 7
Można pokazać uczniom ciekawe własności iloczynów liczb zapisanych za pomocą cyfr 7 i 9 przedstawiając taką oto piramidę iloczynów:
9 ∙ 7 = 63
99 ∙ 77 = 7 6 2 3
999 ∙ 777 = 77 6 22 3
9999 ∙ 7777 = 777 6 222 3
Szyfrowanie liczby 7
Kryptonim 7 można zapisywać w różnych postaciach. Przykładem są takie zadania:
Zadanie 1
Zapisz liczę 7 przy pomocy samych dwójek i znaków działań matematycznych.
Odpowiedź: 7 = 2 + 2 : 2 + 2 ∙ 2
Zadanie 2
Zapisz liczbę 7 za pomocą trójek, dwójek i znaków matematycznych
Odpowiedź:
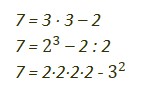
2. Metamorfozy i alkohole
Fizycy potrafią wodę zamienić w wino. Na matematyce można zrobić to samo tylko mocą umysłu. Wykorzystamy tu metamorfozy, czyli łamigłówki słowne, które polegają na przekształceniach danego wyrazu na inny, również sensowny, za pomocą zamiany jednej litery. Nie wolno zmieniać kolejności liter i trzeba pamiętać, aby każde słowo miało jakiś sens. Tym prostym sposobem można zamienić WODĘ w WINO. Metamorfozy prowadzą do istotnych problemów matematycznych. Można je sprowadzić do problemu z teorii grafów. Wierzchołki grafu (punkty) to słowa, krawędzie (linie) to połączenia miedzy słowami. Dwa słowa uznajemy za połączone, jeżeli różnią się jedną literą. Wszystkie łamigłówki sprowadzają się do pytania, czy istnieje jakaś ścieżka w sieci wszystkich możliwych słów czteroliterowych łącząca początkowy i końcowy wyraz.
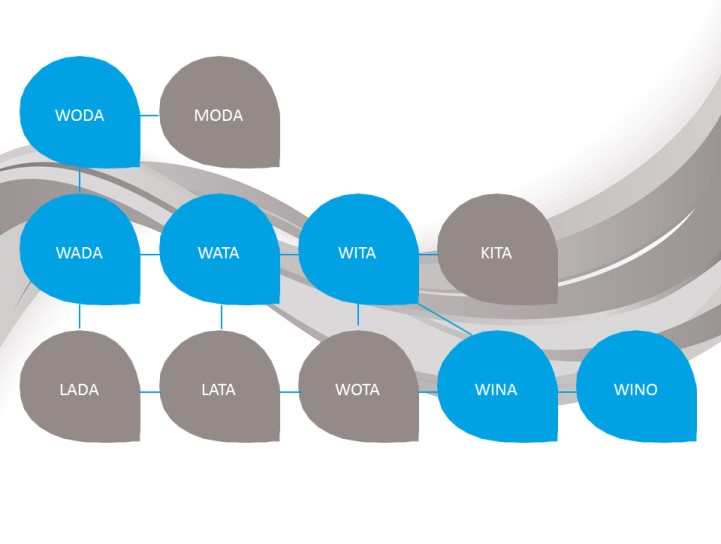
Możliwe ścieżki podczas metamorfozy wyrazu WODA: WODA – WADA – WATA – WITA – WINA – WINO
Wino winem, ale ulubionym drinkiem Bonda jest martini z wódką. Wystarczy w dość znanej zagadce matematycznej zmienić nazwy cieczy i nowa wersja (tylko dla dorosłych) dotyczy drinka agenta 007:
Zadanie 3
Mamy dwie szklanki: jedna pełna wódki, druga pełna martini. Nabieramy łyżeczkę wódki, wlewamy do szklanki z martini i mieszamy. Następnie tą samą łyżeczką nabieramy tę mieszankę i z powrotem przelewamy do szklanki z wódką. Czego jest więcej wódki w martini, czy martini w wódce?
Odpowiedź: jest tyle samo.
3. Rachunek prawdopodobieństwa
Rachunek prawdopodobieństwa do końca XIX wieku uważany był za dział fizyki. Analizie poddawano wyniki prostych doświadczeń polegających na rzucie kostką lub monetą. Do rozwoju tej dziedziny wiedzy przyczynił się w dużej mierze hazard i matematycy, którzy z hazardu czerpali wymierne korzyści. Dla przykładu Mikołaj Bernoulli na balach na dworze cara Piotra I przyjmował zakłady, że na sali znajdują się dwie osoby, które urodziły się tego samego dnia i tego samego miesiąca. Wiele nie ryzykował. Jeżeli na sali znajdowało się 31 osób prawdopodobieństwo wygranej przekraczało ½. Każda następna osoba zwiększała jego szansę na wygraną (patrz wykres poniżej).
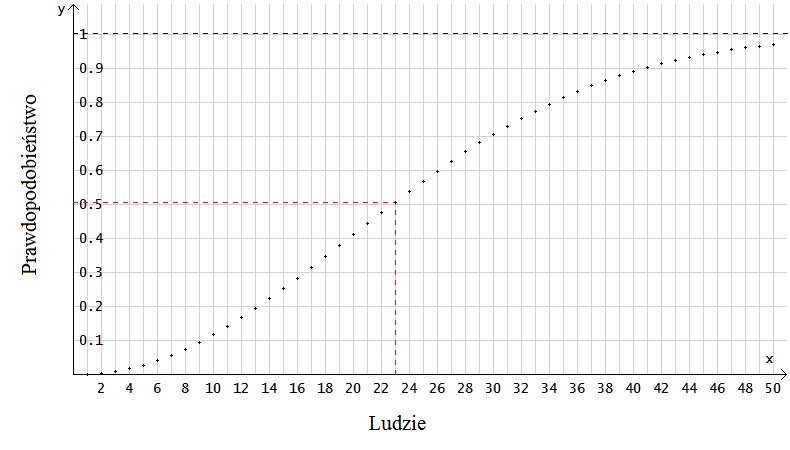
http://pl.wikipedia.org/wiki/Paradoks_dnia_urodzin
Szacowanie
Codziennie jesteśmy zarzucani informacjami, w których występują liczby z wieloma zerami, ale tak naprawdę niewielu ludzi zdaje sobie sprawę z ich obiektywnej wielkości. Szacowanie różnych wielkości jest potrzebną umiejętnością i powinno się ją ćwiczyć, chociażby po to, aby sprawdzić na ile są sensowne. Również w odniesieniu do prawdopodobieństwa nasza intuicja często nas zawodzi. Wiele zależy od sformułowania problemu.
Wyobraźmy sobie, że w dowolnym miejscu na trasie z Opola do Pragi wbijamy deskę szerokości dwóch centymetrów i wysokości dwóch metrów. Niech tą trasą ciemną nocą podróżuje sam James Bond, który w dowolnym momencie wyciąga pistolet i strzela w kierunku pobocza. Trudno byłoby znaleźć kogoś kto postawiłby chociaż złotówkę na to, że trafi w deskę, nawet gdyby za trafienie płacono milion złotych. Tymczasem miliony naszych rodaków systematycznie odwiedza kolektury totolotka w nadziei trafienia szóstki, mimo iż szansa jej trafienia jest zbliżona do trafienia w deskę – około 1 do 14 milionów.
W pewnym okresie bardzo popularny był tak zwany „łańcuszek szczęścia”. Adresat otrzymywał list mniej więcej takiej treści: … przepisz ten list 10 razy usuwając pierwsze nazwisko i dopisując na końcu (na dziesiątym miejscu) swoje. Osobie na miejscu pierwszym wyślij 10 złotych. Już wkrótce na twój adres zaczną wpływać pieniądze ( tu zwykle był opis szczęściarzy, którzy stali się bogaczami). Jeśli przerwiesz ten łańcuszek to, …(tu następował opis różnych nieszczęść, które miały dotknąć nierzetelnego adresata listu).
Zadanie 4
Ile osób musiałoby wziąć udział w łańcuszku szczęścia, aby na adres osoby, która dopisze się na dziesiątym miejscu zaczęły napływać pieniądze ?
Odpowiedź: 11 111 111 110
Kostki do gry, własności brył platońskich
Hazard towarzyszył naszej cywilizacji od zawsze. W latach dwudziestych XX wieku podczas prac wykopaliskowych w sumeryjskim mieście Ur odnaleziono plansze i kostki do gry w kształcie czworościanów foremnych sprzed prawie 5000 lat. Kości to prawdopodobnie najstarsze znane człowiekowi narzędzie służące do gry Używano ich przez wieki zarówno do gier jak i wróżb. Najpopularniejsze stały się kostki sześcienne o krawędzi długości 1 – 2 cm, ze ściankami oznaczonymi kolejnymi cyframi od 1 do 6 lub o odpowiedniej liczbie oczek rozmieszczonych tak, aby suma liczb (oczek) z przeciwległych ścianek wynosiła 7. W założeniu prawdopodobieństwo uzyskania każdego z sześciu wyników powinno być identyczne. Typowe kostki do gier nie są jednak idealnie wyważone. Profesjonalne, stosowane w kasynach mają idealnie gładkie ściany i ostre krawędzie, oczka są drążone, a następnie wypełniane substancją o masie identycznej jak usunięty materiał. Popularne gry fabularne i strategiczne spowodowały rozpowszechnienie się kostek wielościennych. Nie jest to jednak nowość, bo kostki wielościenne były znane już dawniej. W 2003 roku sprzedano na aukcji dwudziestościenną kostkę szklaną pochodzącą z czasów Imperium Rzymskiego. W matematyce rzetelna kostka do gry to taka, która ma jednakową szansę upadku na dowolną swoją ścianę. Każda z brył platońskich może służyć jako rzetelna kostka do gry.

Zadanie 5
a. Jaką kostkę wybierzesz spośród brył platońskich aby mieć największą szansę wylosowania jedynki, dwójki, szóstki, dziesiątki, …
Odpowiedź: wylosowanie jedynki lub dwójki – wybieramy czworościan foremny
szóstki – ośmiościan foremny, dziesiątki – dwunastościan foremny
b. Jaka jest szansa wylosowania jedynki (trójki, szóstki …) w rzucie kostką w kształcie czworościanu foremnego, ośmiościanu foremnego, …
Odpowiedź: szansa wylosowanie jedynki, dwójki, trójki, czwórki w rzucie kostką w kształcie czworościanu foremnego to ¼, szansa wylosowania jedynki, dwójki, …, ósemki w rzucie kostką w kształcie ośmiościanu foremnego to 1/8 itd
Jak grać, żeby wygrać
Szczęściu czasami można pomóc. Tak, jak w anegdocie o władcy, który podróżując przez swoje włości w pewnej miejscowości zauważył płoty i ściany stodół zapełnione rysunkami tarcz ze strzałami wbitymi idealnie w środek. Zapragnął poznać znakomitego strzelca. Strzelcem okazał się mały chłopiec. Zapytany o swoje niezwykłe umiejętności odparł: „To proste. Najpierw strzelam, a potem maluję tarczę”.
W innych przypadkach może przydać się znajomość elementarnej matematyki.
Przykładem może być prosta gra dla dwóch osób, w której matematyka gwarantuje wygraną. Kładziemy 13 cukierków i plasterek cytryny. Każdy z graczy może wziąć jeden, dwa lub trzy cukierki. Gracze sięgają po cukierki kolejno. Przegrywa oczywiście ten, dla którego zostaje cytrynka. Strategia tej gry jest prosta do odkrycia, jeśli ustawimy cukierki w trzech kolumnach:

Łatwo zauważyć, że aby wygrać należy wziąć tyle cukierków, by zawsze naszemu przeciwnikowi pozostała pełna kolumna cukierków (liczba pozostawionych cukierków musi być podzielna przez 4 to jest: 12, 8, 4).
4. Symetrie i asymetrie
Gdzie bawią się światowcy? Oczywiście w kasynie, a w kasynie ruletka, karty – wspaniałe obiekty do rozważań matematycznych na różnym poziomie. Za pomocą matematycznych własności kart można na przykład odgadnąć jedną wybraną kartę (poniżej jeden ze sposobów podany w zbiorze Mechanemata)
Odgadywanie jednej wybranej karty Sztuczkę wykonujemy wybierając z talii karty „niesymetryczne”. Takimi kartami będą: trójki, piątki, szóstki, siódemki, ósemki i dziewiątki kolorów pik, kier i trefl

Wybrane karty układamy tak, aby elementy niesymetryczne były ułożone w jednym kierunku, na przykład tak jak na rysunku:

Tasujemy karty i prosimy kogoś o wyciągniecie jednej karty i zapamiętanie jej. Wyciągniętą kartę wkładamy do reszty talii tak, aby element niesymetryczny był położony odwrotnie, niż w pozostałych kartach. Wówczas łatwo odgadniemy jaka karta została wyciągnięta, gdyż tylko na niej element niesymetryczny będzie położony odwrotnie.

Autor: Aleksandra Opaska
Literatura:
[1]. Marcus Du Sautoy;„Poker z Pitagorasem”, Carta Blanca Sp.z o.o. Grupa Wydawnicza PWN, Warszawa 2012
[2]. Ian Steward; Gabinet matematycznych zagadek, część II, Wydawnictwo Literackie, Kraków 2012
[3]. Christoph Drosser; MATEMATYKA daj się uwieść, Wydawnictwo Naukowe PWN, Warszawa 2011
[4]. Szczepan Jeleński; Lilavati, WSiP, Warszawa 1982
[5]. John D. Barrow; Jak wygrać na loterii?, Wydawnictwo Literackie, Kraków 2011
[6]. www.matematyka.wroc.pl/doniesienia/gry-losowe
[7]. www.wikipedia.org
Publikowane:
[1]. Bujak B. Ociepa M. Opaska A. Raczkowska-Tomczak K. Tomalak A.; „I am Bond. Science Bond…” Veletrh Napadu Ucitelu Fyziky18, sbornik z konference, Hradec Kralove 2013, s. 223-239 http://vnuf.cz/sbornik/rocniky/
[2]. Bujak B. Ociepa M. Opaska A. Raczkowska-Tomczak K. Tomalak A.; Biuletyn Polskiego Stowarzyszenia Nauczycieli Przedmiotów Przyrodniczych; „I am Bond, Science Bond…”, Nauczanie Przedmiotów Przyrodniczych, tom 46, 2/2013, Toruń 2013, s.30-39
Prezentowane:
[1]. Konferencja dla nauczycieli fizyki „Veletrh Napadu Ucitelu Fyziky18”, Hradec Králové, 30. 8. – 1. 9. 2013
https://slideplayer.cz/slide/835798/
[2]. XX Ogólnopolski Zjazd PSNPP, Toruń 20-22.09.2013
[3]. Konwersatorium popularyzacji wiedzy, Wydział Matematyczno-Fizyczno-Techniczny Uniwersytetu Pedagogicznego w Krakowie 20.11.2013
[4]. XIII Opolski Festiwal Nauki, Noc Nauki, 29.05-1.06.2015
