Wbrew powszechnemu mniemaniu matematyka jest wokół nas, a zagadnienia matematyczne mogą dotyczyć różnych zjawisk. Na różne przedmioty można spojrzeć z punktu widzenia matematyki.
Zwykła kartka papieru może stać się inspiracją dla rozważań matematycznych. Treści i zadania związane z kartką papieru należy oczywiście dostosować do wieku i umiejętności uczestników zajęć.
I. Wymiary kartki papieru.
Uczniowie doskonale wiedzą, że kartki jakich używają, na przykład na plastyce, to kartki A4, mniejsze to A5, większe A3. Mało kto jednak wie, że w wymiarach kartek formatu A kryje się pierwiastek z dwóch .Składając kartkę A0 na pół wzdłuż dłuższego boku otrzymujemy dwie kartki A1, składając w ten sam sposób kartkę A1 otrzymujemy A2 i tak dalej. W ten sposób otrzymujemy arkusze o takiej samej proporcji boków jak arkusz wyjściowy.
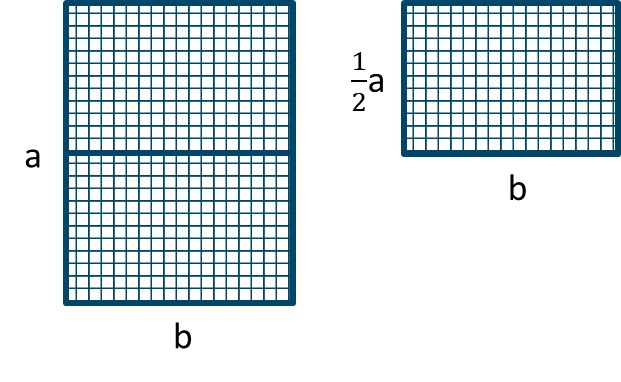
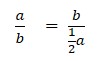
iloczyn wyrazów skrajnych jest równy iloczynowi wyrazów środkowych, stąd po przekształceniu otrzymujemy:
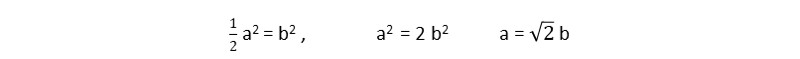
W kartkach formatu A dłuższy bok kartki jest ![]() razy większy od długości krótszego boku w zaokrągleniu do pełnych milimetrów.
razy większy od długości krótszego boku w zaokrągleniu do pełnych milimetrów.
II. Składanie kartki papieru.
Ciekawa i często zaskakująca jest odpowiedź na pytanie: ile razy można złożyć na pół kartkę papieru?
Ćwiczenie 1. Złóż kartkę papieru jak najwięcej razy.
Uczestnicy zajęć prognozują ile razy złożą „na pół” kartkę A4?
Następnie indywidualnie składają kartki i konfrontują prognozy z otrzymanymi wynikami. Starszym dzieciom można zaproponować wykonanie odpowiednich obliczeń i wtedy okazuje się, że po ósmym złożeniu nasza kartka byłaby grubsza, niż dłuższa, bo jej długość wynosiłaby niecałe półtora milimetra, za to grubość ponad centymetr (długość: 1,25 mm, grubość: 12,8 mm)
Przez dłuższy czas za rekord uznawano złożenie kartki 7 razy i taki wynik zwykle otrzymują uczniowie. W 2002 roku Britney Gallivan, uczennica z Pomona w Kalifornii, złożyła papier aż 12 razy. Nie składała jednak kartki A4, tylko mocny papier toaletowy.
W 2012 roku studenci z St. Mark’s School w Southborough w stanie Massachusetts w „niekończącym się” korytarzu na Massachusetts Institute of Technology złożyli papier 13 razy uzyskując tym sposobem blok szeroki na 1,5 metra i wysoki na 76 cm, który zawierał aż 8192 warstwy papieru. Relacja z tego wydarzenia może być inspiracją dla uczniów, a próba bicia szkolnego rekordu może być początkiem ciekawej lekcji.

Praktyczna granica składania papieru na pół to zapewne ta, ustalona przez studentów z St. Mark’s School. Dalej kartkę papieru można składać już tylko teoretycznie. Problemem tym zajmował się argentyński profesor i popularyzator matematyki Adrian Paenza, którego obliczenia są dla nas zaskakujące. Można poprosić uczniów o oszacowanie, jaką grubość miałaby kartka papieru złożona 17, 25, 40 czy 45 razy? Grubość warstwy papieru złożonego 25 razy jest porównywalna z wysokością najwyższych budynków, warstwa uzyskana w wyniku 40 krotnego złożenia jest porównywalna z wysokością na jakiej krążą nadajniki GPS, a teoretyczny blok papieru złożonego na pół 45 razy sięgnąłby księżyca. Grubość warstwy papieru zwiększa się bowiem 2n razy, gdzie n oznacza liczbę złożeń i opisuje ją funkcja wykładnicza.

III. Długość kartki papieru. Wyzwaniem dla uczniów może być zadanie polegające na wykonaniu w kartce A5 takiego otworu, żeby było możliwe było przełożenie jej przez głowę i przejście na jej drugą stronę.
Ćwiczenie 2. Przejdź przez kartkę papieru formatu A5.

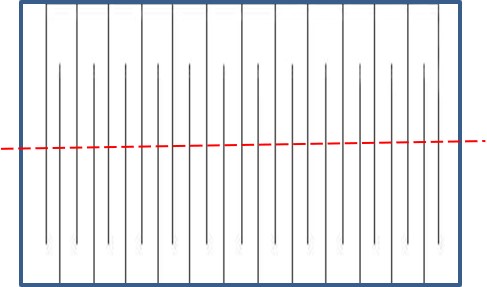
Zadanie jest możliwe do wykonania po odpowiednim nacięciu złożonej kartki wg szablonu. Wystarczy kartkę złożyć na pół i ponacinać ją (byle nie do końca! ) raz z jednej, a raz z drugiej strony. Następnie ostrożnie rozłożyć i gotowe.
IV. Super moc kartki papieru.
Czy papier jest materiałem wytrzymałym? Pierwsza odpowiedź zwykle jest negatywna, bo kartkę papieru bardzo łatwo jest przerwać , ale z kartką złożoną kilkukrotnie nie jest już tak łatwo.
Ćwiczenie 3. Z kartki A4 wykonaj podporę pod deseczkę tak, aby deseczka oparta na podporach znalazła się co najmniej 4 cm ponad podłożem i utrzymała maksymalnie duży ciężar. Uczestnicy zajęć zgłaszają różne propozycje. Najefektywniejsze rozwiązanie to przecięcie kartki na 4 na cztery równej szerokości paski i zwinięcie ich w ruloniki, które sklejamy taśmą klejącą.

V . Geometria kartki papieru.
Ciekawe i pouczające może być składanie kartki papieru. Inspiracją może być na przykład propozycja opisana na stronie Matematyka TV http://matematyka.boo.pl/readarticle.php?article_id=19
Doswiadczenie polega na składaniu kartki A4 w taki sposób, że otrzymujemy kolejno: trójkąt równoboczny i jego wysokości, środek okręgu wpisanego i opisanego na tym trójkącie, trapez równoramienny, romb, trójkąt równoboczny, czworościan foremny, sześciokąt foremny, wreszcie gwiazdę.
Nie musimy zresztą składać całej kartki. Możemy ograniczyć się do paska papieru, a wtedy skonstruować możemy pięciokąt foremny. Sam pasek papieru stwarza nam pole do działania podczas następnych zajęć . Mogą być to na przykład zagadnienia związane z malowaniem czy cięciem wstęgi Mobiusa.
Bibliografia:
[2]. http://matematyka.boo.pl/readarticle.php?article_id=19
[3]. http://www.spryciarze.pl/zobacz/jak-wykonac-10-niesamowitych-sztuczek-z-papierem
[4]. http://www.crazynauka.pl/kartka-zlozona-103-razy-bylaby-grubsza-niz-wszechswiat
[5]. http://matematyka.boo.pl/readarticle.php?article_id=19
Autor: Aleksandra Opaska
Publikowane:
Opaska Aleksandra; Biuletyn Polskiego Stowarzyszenia Nauczycieli Przedmiotów Przyrodniczych , „Porozmawiajmy o kartce papieru na matematyce”, Nauczanie Przedmiotów Przyrodniczych, nr 64 (4/2017),Toruń 2017, s. 38-40
Prezentowane podczas warsztatów prowadzonych na XXIV Zjeździe PSNPP nt. „Wyzwania współczesnej energetyki”, który odbył się 25-27 sierpnia 2017 roku w Opolu.
